Day 17: Greedy Isn’t Always Bad: Heuristics in Genetic Algorithms

Genetic algorithms thrive on randomness and gradual improvement, but randomness alone often leads to slow convergence. While global search is essential to explore the full solution space, local improvements can dramatically accelerate progress. That is where heuristics come into play. Specifically, greedy heuristics can guide genetic algorithms by introducing problem-specific knowledge that favors better starting points, smarter offspring, and faster convergence.

Contrary to the purist view that GAs should remain entirely stochastic, adding domain-aware strategies like greedy initialization, greedy mutation, or repair heuristics can significantly boost performance in complex problems such as the Traveling Salesperson Problem, scheduling, or layout optimization.

Let’s take a closer look at how greedy logic can complement evolutionary search and where it can be integrated into your C# GA implementations.

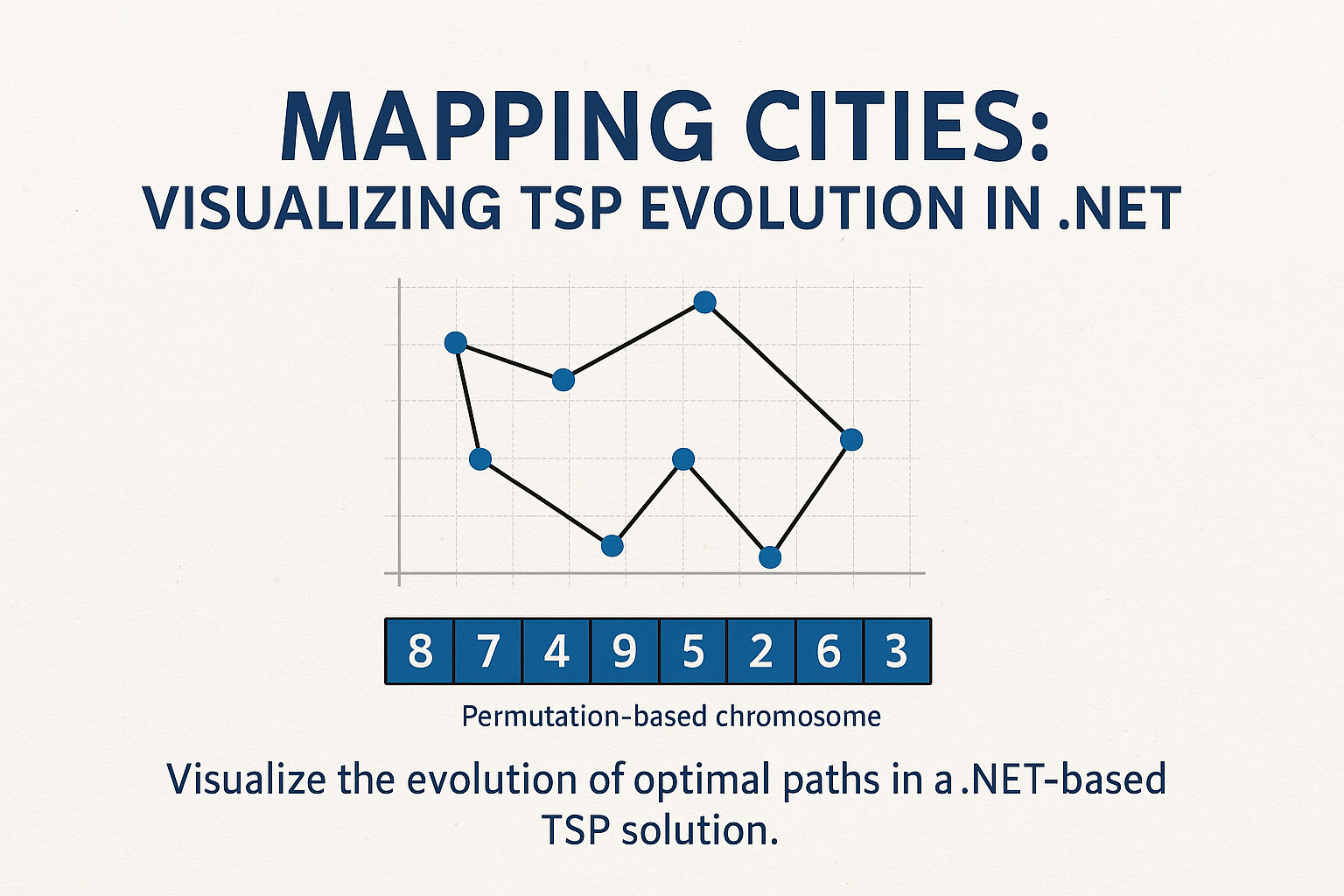
Start with the initial population. Instead of generating every chromosome randomly, you can seed part of the population using a greedy algorithm that constructs a decent solution based on immediate cost decisions.

For TSP, this might involve starting from a random city and always choosing the nearest unvisited neighbor:

public static int[] GreedyTour(double[,] distances, int startCity)
{
    int cityCount = distances.GetLength(0);
    var visited = new bool[cityCount];
    var tour = new int[cityCount];
    tour[0] = startCity;
    visited[startCity] = true;

    for (int i = 1; i < cityCount; i++)
    {
        int last = tour[i - 1];
        double minDist = double.MaxValue;
        int nextCity = -1;

        for (int j = 0; j < cityCount; j++)
        {
            if (!visited[j] && distances[last, j] < minDist)
            {
                minDist = distances[last, j];
                nextCity = j;
            }
        }

        tour[i] = nextCity;
        visited[nextCity] = true;
    }

    return tour;
}

Use this function to seed a portion of your population during initialization:

for (int i = 0; i < populationSize; i++)
{
    int[] genes = i < populationSize / 4
        ? GreedyTour(distanceMatrix, i % cityCount)
        : RandomTour(cityCount);

    population.Add(new PermutationChromosome(genes));
}

This hybrid approach creates a diverse population with a few high-quality initial candidates that help guide early generations.

You can also use greedy logic within mutation operations. Suppose you mutate a chromosome and want to improve its local structure. After mutation, you can run a simple 2-opt local search to remove obvious route inefficiencies:

public void TwoOptLocalSearch(double[,] distances)
{
    bool improvement = true;
    while (improvement)
    {
        improvement = false;
        for (int i = 1; i < Genes.Length - 2; i++)
        {
            for (int j = i + 1; j < Genes.Length; j++)
            {
                double before = distances[Genes[i - 1], Genes[i]] + distances[Genes[j], Genes[(j + 1) % Genes.Length]];
                double after = distances[Genes[i - 1], Genes[j]] + distances[Genes[i], Genes[(j + 1) % Genes.Length]];

                if (after < before)
                {
                    Array.Reverse(Genes, i, j - i + 1);
                    improvement = true;
                }
            }
        }
    }
}

Use this after crossover or mutation on a small percentage of chromosomes to clean up inefficient gene segments. This type of local optimization is greedy because it always takes the best immediate improvement, but it works extremely well when integrated into global search.

Another opportunity to apply greedy heuristics is in repairing infeasible solutions. In problems like scheduling, mutations can cause constraint violations. You can use greedy logic to detect and fix these violations efficiently while preserving the core of the chromosome. For example, if a job is scheduled twice, you could replace the duplicate with the next available job in a greedy manner.

Greedy operators can also guide crossover. Instead of randomly mixing parent genes, you can construct a child by greedily selecting the next best gene from either parent, based on the shortest edge or lowest cost:

public static int[] GreedyCrossover(int[] parent1, int[] parent2, double[,] distances)
{
    var remaining = new HashSet<int>(parent1);
    var tour = new List<int> { parent1[0] };
    remaining.Remove(parent1[0]);

    while (remaining.Count > 0)
    {
        int last = tour[^1];
        int next1 = GetNextCity(parent1, last, remaining);
        int next2 = GetNextCity(parent2, last, remaining);

        double d1 = next1 >= 0 ? distances[last, next1] : double.MaxValue;
        double d2 = next2 >= 0 ? distances[last, next2] : double.MaxValue;

        int next = d1 < d2 ? next1 : next2;
        tour.Add(next);
        remaining.Remove(next);
    }

    return tour.ToArray();
}

private static int GetNextCity(int[] parent, int current, HashSet<int> remaining)
{
    int index = Array.IndexOf(parent, current);
    for (int i = index + 1; i < parent.Length; i++)
    {
        if (remaining.Contains(parent[i]))
            return parent[i];
    }
    for (int i = 0; i < index; i++)
    {
        if (remaining.Contains(parent[i]))
            return parent[i];
    }
    return -1;
}

This greedy crossover combines useful subsequences from both parents while maintaining feasibility.

Greedy methods are especially powerful when applied selectively. Use them to generate better starting populations, refine children, or maintain valid solutions. The key is not to replace global search with greedy logic, but to complement it. Evolution needs randomness to discover new ideas and greedy heuristics to refine them efficiently.

By integrating greedy decisions at critical points, your genetic algorithm becomes more than just an evolutionary system. It becomes a strategic search engine that balances global exploration with local exploitation. When used carefully, greedy isn’t just acceptable. It’s smart.